迷人的完全數﹝註1﹞

列志佳

完全數是一些特殊的自然數，它所有的真因數（即除了自身以外的因數）的和，恰好等於它本身。例如 的真因數有 ，而 ，所以 是完全數；又如 的真因數有 ，但 ，所以 不是完全數。首五個完全數分別為 和 。

我早年已被完全數多項漂亮的性質所吸引﹝註2﹞，可謂嘆為觀止，深感非常值得老師們向中小學生介紹，讓他們欣賞數學之美！﹝註3﹞部分定理的證明不太深奧，老師更可向對數學較感興趣的中學生作進一步解說，提升他們對數學的興趣。再加上至今仍無人能破解「是否有無限多個完全數？」、「是否存在奇完全數？」兩大古老數論難題，對學生來說，更顯其魅力！

早前，我在學習的過程中，完成了一份小習作﹝註4﹞，推導出「 是唯一一個為其真因數之和及積之正整數」。即在無限多個自然數中，只有 這個完全數才可以同時間為其真因數之和及積 ( )。恰巧 為首三個連續自然數，故上式更顯奇妙，令人著迷！

「數學，如果正確地看它，不但擁有真理，而且也具有至高的美。」﹝註5﹞我多年來被數學的簡潔美、和諧美、對稱美、抽象美、永恆美所吸引，教學時亦盡力把握良機，引導學生欣賞數學所呈現的美。一旦學生能懂得從審美的角度來欣賞數學，自能激發其內在動機，令他自發努力研習這門偉大而優雅的學問。

從漂亮程度來看，讓學生初步認識完全數，不正是一個不錯的嘗試嗎？

註1：本文得黃毅英先生啟發而成，謹此致謝！

註2：舉例如下：

每個偶完全數都可以寫成連續自然數之和，即每個偶完全數均是三角形數。

除6以外的偶完全數，均可以表示成連續奇立方數之和。

所有的偶完全數都可以表達為2的一些連續正整數次冪之和。

每個完全數的所有因數（包括本身）的倒數之和，都等於2。

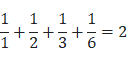
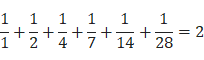
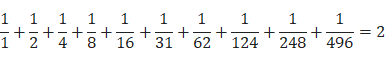
偶完全數都是以6或28結尾等。

詳情可參考下列網上資料或文獻：

https://zh.wikipedia.org/wiki/%E5%AE%8C%E5%85%A8%E6%95%B0

https://web.math.sinica.edu.tw/math_media/d213/21302.pdf

https://math.dartmouth.edu/~jvoight/notes/perfelem.pdf

註3：筆者以前多利用連堂之間的小休時間，與學生分享一些課程以外的數學小知識、數學史和數學家的故事。一則那段時間較為輕鬆，二則可讓學生自選是否收聽，結果也吸引到一些學生專心聆聽。在正式的課堂時間內，當然也可「間中」滲入這類「題外話」，部分學生也喜歡細聽。但正因本港課程緊迫，若老師時常在這時段作分享，部分學生或許有少許反感，可能弄巧反拙，不可不慎。

註4：http://kyyeung.synology.me/Sharing/lit-21/beauty-six.pdf

註5：語出自英國哲學家、數學家和邏輯學家羅素（Bertrand Arthur William Russell，）。

8-4-2023